Мундариҷа

• Ба қадам
• Усули 1 аз 3: Истифодаи формулаҳои радиус
• Усули 2 аз 3: Мафҳумҳои калидиро муайян кунед
• Усули 3 аз 3: Пайдо кардани радиус ҳамчун масофаи байни ду нуқта
• Маслиҳатҳо

Радиуси кура (кӯтоҳ ҳамчун тағирёбанда р ё Р.) масофа аз маркази дақиқи кура ба нуқтаи сатҳи он кура аст. Тавре ки дар доираҳо, радиуси кура аксар вақт барои ҳисоб кардани диаметри, даврӣ, масоҳат ва ҳаҷми кура ченаки муҳим мебошад. Аммо, шумо метавонед инчунин аз диаметри, даврашакл ва ғ. Ба қафо кор карда, радиуси сфераро ёбед. Формулаеро, ки барои маълумоти дар даст доштаатон мувофиқ аст, истифода баред.

Ба қадам

Усули 1 аз 3: Истифодаи формулаҳои радиус

1. Агар шумо диаметро донед, радиусро муайян кунед. Радиус ним диаметр аст, бинобар ин шумо формуларо истифода мебаред r = D / 2. Ин ба усули ҳисоб кардани радиуси давра, ки диаметри он дода шудааст, шабеҳ аст.
   • Агар шумо курраи диаметраш 16 см дошта бошед, радиусро бо 16/2 = ҳисоб мекунед 8 см. Агар диаметри он 42 бошад, пас радиусаш он аст 21.
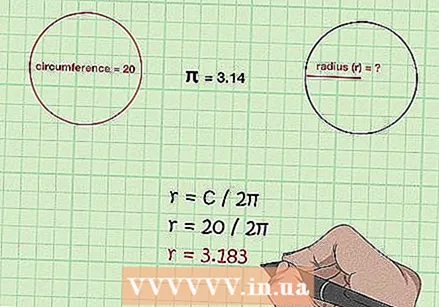2. Агар шумо давраро медонед, радиусро муайян кунед. Формуларо истифода баред C / 2π. Азбаски давра ба πD баробар аст ва он дар навбати худ ба 2πr баробар аст, радиусро бо тақсим кардани атроф ба 2π ҳисоб кунед.
   • Агар шумо курраи атрофиаш 20 м дошта бошед, радиусашро бо 20 / 2π = 3.183 м.
   • Шумо метавонед ҳамон формуларо барои табдилдиҳӣ дар байни радиус ва гирду атрофи давра истифода баред.
3. Агар шумо ҳаҷми курро донед, радиусро ҳисоб кунед. Формулаи ((V / π) (3/4)) -ро истифода баред. Ҳаҷми кура аз муодилаи V = (4/3) πr бароварда мешавад. Ҳангоми ҳалли муодилаи r, шумо ((V / π) (3/4)) = r ба даст меоред, аз ин рӯ маълум мешавад, ки радиуси a ё кура ба ҳаҷме, ки ба 3 тақсим карда шудааст, 3/4 маротиба, ба қудрати 1/3 (ё решаи кубӣ).
   • Агар шумо куррае дошта бошед, ки ҳаҷмаш 100 см аст, радиусро ба таври зерин мегиред:
     • ((V / π) (3/4)) = r
     • ((100 / π) (3/4)) = r
     • ((31.83) (3/4)) = r
     • (23.87) = р
     • 2,88 = r
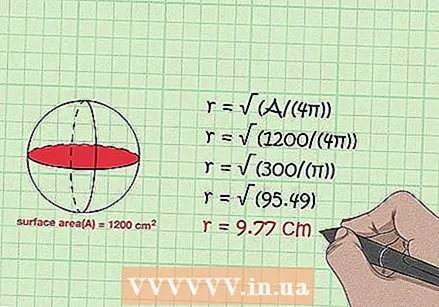4. Радиуси сатҳро муайян кунед. Формуларо истифода баред r = √ (A / (4π)). Шумо масоҳати кураро бо муодилаи A = 4πr ҳисоб мекунед. Ҳалли муодилаи барои r √ (A / (4π)) = r медиҳад, ки маънои радиуси шар ба решаи квадратии майдони он ба 4 by тақсимшуда баробар аст. Шумо инчунин метавонед барои натиҷаи якхела (A / (4π)) -ро ба 1/2 барқ ​​диҳед.
   • Агар шумо курае дошта бошед, ки масоҳаташ 1200 см бошад, радиусро чунин ҳисоб мекунед:
     • √ (A / (4π)) = r
     • √ (1200 / (4π)) = r
     • √ (300 / (π)) = r
     • √ (95.49) = r
     • 9.77 см = r

Усули 2 аз 3: Мафҳумҳои калидиро муайян кунед

1. Андозаҳои асосии кураро бидонед. Радиус (р) масофа аз маркази дақиқи кура то нуқтаи рӯи кура мебошад. Умуман, шумо метавонед радиуси кураро пайдо кунед, агар шумо диаметри, атроф, ҳаҷм ё масоҳати онро донед.
   • Диаметри (D): дарозии хат тавассути маркази сфера & ndash; радиусро дучанд кунед. Диаметри дарозии хате тавассути маркази кура, аз як нуқтаи берунаи кура то нуқтаи мувофиқи мустақим дар муқобили он мебошад. Ба ибораи дигар, масофаи калонтарини байни ду нуқтаи сфера.
   • Давра (C): масофаи якандоза дар атрофи кура дар нуқтаи васеътарини он. Ба ибораи дигар, гирди буриши даврии кура, ки ҳамвории он аз маркази кура мегузарад.
   • Ҷилди (V): фазои сеандоза дар дохили сфера. Ин "фазои ишғолкардаи соҳа" мебошад.
   • Сатҳӣ (A): фазои дуандоза дар сатҳи берунии кура. Миқдори фазои ҳамвор, ки берунии кураро фаро мегирад.
   • Pi (π): доимӣ, ки таносуби давраро ба диаметри даврро ифода мекунад. 10 рақами аввали Pi ҳамеша ҳастанд 3,141592653, гарчанде ки ин одатан ба мудаввар карда мешавад 3,14.
2. Барои муайян кардани радиус ченакҳои гуногунро истифода баред. Шумо метавонед диаметри, атроф, ҳаҷм ва масоҳатро барои ҳисоб кардани радиуси шар истифода баред. Агар шумо дарозии радиусро донед, шумо метавонед ягонтои ин рақамҳоро ҳисоб кунед. Ҳамин тавр, барои ёфтани радиус шумо метавонед формулаҳои ҳисобкунии ин қисмҳоро баргардонед. Формулаҳои радиусро барои ҳисоб кардани диаметр, атроф, майдон ва ҳаҷм омӯзед.
   • D = 2r. Тавре ки дар доираҳо, диаметри сфера аз радиус ду маротиба зиёдтар аст.
   • C = -D ё 2πr. Тавре ки дар доираҳо, гирди кура ба диаметри π баробар аст. Азбаски диаметри радиус ду маротиба зиёд аст, мо инчунин гуфта метавонем, ки гирду атроф маротиба радиусаш π мебошад.
   • V = (4/3) rr. Ҳаҷми кура радиус ба қувваи куб (r x r x r), маротиба π, маротиба 4/3 мебошад.
   • A = 4πr. Масоҳати кура радиуси қудрати ду (rxr) маротиба π, маротиба 4. аст. Азбаски доираи атроф πr аст, инчунин гуфтан мумкин аст, ки майдони кура ба чор баробар аст масоҳати давраро, ки аз рӯи гирду атрофи он ба вуҷуд омадааст, зиёд мекунад.

Усули 3 аз 3: Пайдо кардани радиус ҳамчун масофаи байни ду нуқта

1. Координатаҳои (x, y, z) маркази сфераро ёбед. Яке аз роҳҳои андеша дар бораи радиуси кура масофаи байни маркази кура ва ҳар нуқтаи рӯи он мебошад. Азбаски ин дуруст аст, шумо метавонед координатҳои марказ ва нуқтаи сатҳи кураро барои муайян кардани радиуси кура бо роҳи ҳисоб кардани масофаи байни ду нуқта бо истифода аз тағирёбии формулаи масофаи стандартӣ истифода баред. Барои оғоз координатҳои маркази сфераро ёбед. Аҳамият диҳед, ки сфера сеандоза аст, ба ҷои (x, y) нуқта (x, y, z) хоҳад буд.
   • Бо мисол фаҳмидани ин осонтар аст. Фарз мекунем, ки шар бо ҳамчун марказ дода шудааст (-1, 4, 12). Дар чанд қадами оянда, мо ин нуктаро ҳангоми муайян кардани радиус истифода хоҳем кард.
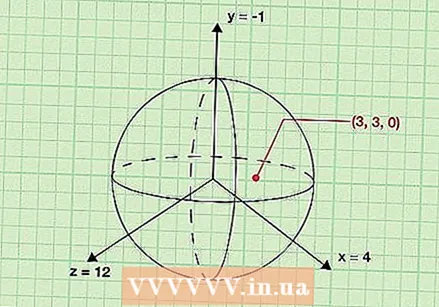2. Координатҳои нуқтаро дар сатҳи кура ёбед. Пас ба шумо лозим аст, ки (x, y, z) координатҳои нуқтаеро дар сатҳи кура муайян кунед. Ин имконпазир аст ҳар як нуқта дар сатҳи кура. Азбаски мувофиқи таъриф ҳамаи нуқтаҳои сатҳи кура аз марказ баробаранд, шумо метавонед ҳар нуқтаро барои муайян кардани радиус истифода баред.
   • Дар заминаи машқи намунавии худ, мо инро қайд мекунем (3, 3, 0) дар сатҳи кура. Бо ҳисоб кардани масофаи байни ин нуқта ва марказ, мо метавонем радиусро пайдо кунем.
3. Бо формулаи d = √ ((x.) Радиусро муайян кунед₂ - х₁) + (y₂ - y₁) + (з₂ - з₁)). Ҳоло, ки шумо маркази кура ва нуқтаеро дар сатҳи курро медонед, шумо метавонед радиусро тавассути ҳисоб кардани масофаи байни онҳо фаҳмед. Формулаи масофаи сеандозаи d = √ ((x.) -Ро истифода баред₂ - х₁) + (y₂ - y₁) + (з₂ - з₁)), ки d масофа аст, (х₁, y₁, з₁) координатҳои марказро ифода мекунад ва (х₂, y₂, з₂) барои муайян кардани масофаи байни ду нуқта координатаҳои нуқтаи сатҳро ифода мекунад.
   • Дар мисоли мо, (4, -1, 12) -ро барои (х.) Иваз мекунем₁, y₁, з₁) ва (3, 3, 0) барои (х₂, y₂, з₂), чунин ҳал мекунад:
     • d = √ ((x₂ - х₁) + (y₂ - y₁) + (з₂ - з₁))
     • d = √ ((3 - 4) + (3 - -1) + (0 - 12))
     • d = √ ((- 1) + (4) + (-12))
     • d = √ (1 + 16 + 144)
     • d = √ (161)
     • г = 12.69. Ин радиуси соҳаи мост.
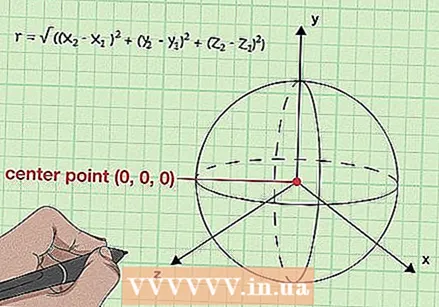4. Умуман, бидонед, ки r = √ ((x₂ - х₁) + (y₂ - y₁) + (з₂ - з₁)). Дар кура, ҳар як нуқтаи сатҳ аз маркази кура яксон аст. Бо назардошти формулаи масофаи сеандозаи боло ва иваз кардани тағирёбандаи "d" бо тағирёбандаи "r" -и радиус, мо муодилае мегирем, ки ба мо имкон медиҳад радиусро дар ҳар нуқтаи маркази додашуда (х₁, y₁, з₁) ва ҳар нуқтаи мувофиқи сатҳи (х.)₂, y₂, з₂).
   • Бо квадрат кардани ҳарду тарафи ин муодила мо ба даст меорем: r = (x₂ - х₁) + (y₂ - y₁) + (з₂ - з₁). Эзоҳ: Ин аслан ба муодилаи стандартии соҳа (r = x + y + z) монанд аст, агар марказ ба (0,0,0) баробар бошад.

Маслиҳатҳо

• Тартиби амалиёт муҳим аст. Агар шумо мутмаъин набошед, ки қоидаҳои ҳисоб чӣ гуна кор мекунанд ва ҳисобкунаки шумо қавсҳоро дастгирӣ мекунад, боварӣ ҳосил кунед, ки онҳоро истифода баред.
• Ин мақола барои он сохта шудааст, ки ба ин мавзӯъ талабот зиёд буд. Аммо, агар шумо бори аввал кӯшиш кунед, ки геометрияи фазоиро фаҳмед, беҳтараш онро аз тарафи дигар оғоз кардан лозим аст: ҳисоб кардани хосиятҳои кура ҳангоми додани радиус.
• Пи ё letter ҳарфи юнонӣ буда, таносуби диаметри давраро ба доираи он нишон медиҳад. Ин адади ғайримантиқӣ аст ва наметавон онро ҳамчун таносуби рақамҳои воқеӣ навишт. Тахминҳо зиёданд ва 333/106 пи-ро ба чор даҳ даҳӣ бармегардонад. Имрӯз аксарияти одамон тақрибан 3.14-ро дар хотир доранд, ки одатан барои мақсадҳои ҳаррӯза дақиқ аст.