Мундариҷа

• Қадамҳо
• Усули 1 аз 3: Чӣ тавр як муодилаи кубиро бидуни мӯҳлати доимӣ ҳал кардан мумкин аст
• Усули 2 аз 3: Чӣ тавр пайдо кардани решаҳои пурра бо истифода аз мултипликаторҳо
• Усули 3 аз 3: Чӣ тавр як муодиларо бо истифода аз дискриминант ҳал кардан мумкин аст

Дар муодилаи кубӣ, нишондиҳандаи баландтарин 3 аст, чунин муодила 3 ​​реша (ҳалли) дорад ва он шакл дорад ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Ҳал кардани баъзе муодилаҳои кубӣ чандон осон нест, аммо агар шумо усули дурустро (бо заминаи хуби назариявӣ) татбиқ кунед, шумо метавонед решаҳои ҳатто муодилаи мураккаби кубиро пайдо кунед - барои ин формулаи ҳалли муодилаи квадратиро истифода баред. решаҳои пурра, ё ҳисоб кардани табъиз.

Қадамҳо

Усули 1 аз 3: Чӣ тавр як муодилаи кубиро бидуни мӯҳлати доимӣ ҳал кардан мумкин аст

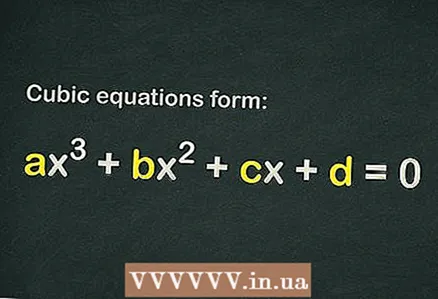1. 1 Бифаҳмед, ки оё дар муодилаи кубӣ истилоҳи озод мавҷуд аст г{ Displaystyle d}. Муодилаи кубӣ шакл дорад ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Барои он ки як муодила куб ҳисобида шавад, танҳо истилоҳ кофист ${ Displaystyle x ^ {3}}$ (яъне умуман аъзои дигар набошанд).
   • Агар муодила мӯҳлати озод дошта бошад ${ Displaystyle d}$, усули дигарро истифода баред.
   • Агар дар муодила ${ Displaystyle a = 0}$, он кубӣ нест.
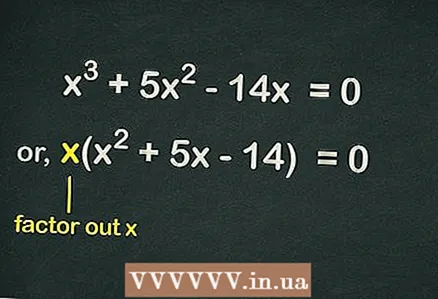2. 2 Аз қавс хориҷ кунед х{ Displaystyle x}. Азбаски дар муодила истилоҳи озод нест, ҳар як истилоҳ дар муодила тағирёбандаро дар бар мегирад ${ Displaystyle x}$... Ин маънои онро дорад, ки як ${ Displaystyle x}$ барои содда кардани муодила метавон аз қавс хориҷ карда шавад. Ҳамин тариқ, муодила чунин навишта мешавад: ${ Displaystyle x (ax ^ {2} + bx + c)}$.
   • Масалан, бо назардошти муодилаи кубӣ ${ Displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Овардан ${ Displaystyle x}$ қавс ва дастрас кунед ${ Displaystyle x (3x ^ {2} -2x + 14) = 0}$
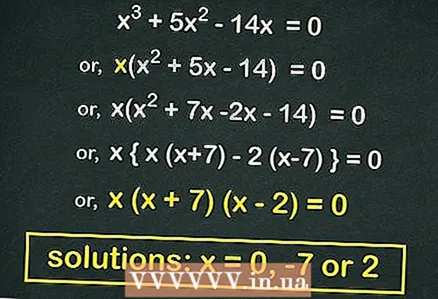3. 3 Омил (маҳсули ду бином) муодилаи квадратӣ (агар имконпазир бошад). Бисёр муодилаҳои квадратии шакл ${ displaystyle ax ^ {2} + bx + c = 0}$ омил кардан мумкин аст. Агар мо онро барорем, чунин муодила пайдо мешавад ${ Displaystyle x}$ берун аз қавс. Дар мисоли мо:
   • Аз қавс хориҷ кунед ${ Displaystyle x}$: ${ Displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Омили муодилаи квадратӣ: ${ Displaystyle x (x + 7) (x-2) = 0}$
   • Ҳар як бинро ба баробар кунед ${ Displaystyle 0}$... Решаҳои ин муодила дар онанд ${ Displaystyle x = 0, x = -7, x = 2}$.
4. 4 Бо истифода аз формулаи махсус муодилаи квадратиро ҳал кунед. Ин корро кунед, агар муодилаи квадратиро ба факторизатсия кардан имконнопазир бошад. Барои ёфтани ду решаи муодила, қиматҳои коэффисиентҳо ${ Displaystyle a}$, ${ Displaystyle b}$, ${ Displaystyle c}$ дар формула иваз кунед ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • Дар мисоли мо, қиматҳои коэффисиентҳоро иваз кунед ${ Displaystyle a}$, ${ Displaystyle b}$, ${ Displaystyle c}$ (${ Displaystyle 3}$, ${ Displaystyle -2}$, ${ Displaystyle 14}$) ба формула:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • Решаи аввал:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • Решаи дуюм:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Решаҳои сифр ва квадратиро ҳамчун ҳалли муодилаи куб истифода баред. Муодилаҳои квадратӣ ду реша доранд, дар ҳоле ки муодилаҳои кубӣ се реша доранд. Шумо аллакай ду ҳалли худро ёфтаед - ин решаҳои муодилаи квадратӣ мебошанд. Агар шумо "x" -ро берун аз қавс гузоред, роҳи сеюм чунин хоҳад буд ${ Displaystyle 0}$.
   • Агар шумо "x" -ро аз қавс хориҷ кунед, шумо мегиред ${ Displaystyle x (ax ^ {2} + bx + c) = 0}$, яъне ду омил: ${ Displaystyle x}$ ва муодилаи квадратӣ дар қавс. Агар яке аз ин омилҳо бошад ${ Displaystyle 0}$, тамоми муодила низ ба баробар аст ${ Displaystyle 0}$.
   • Ҳамин тариқ, ду решаи муодилаи квадратӣ ҳалли муодилаи кубӣ мебошанд. Ҳалли сеюм ин аст ${ Displaystyle x = 0}$.

Усули 2 аз 3: Чӣ тавр пайдо кардани решаҳои пурра бо истифода аз мултипликаторҳо

1. 1 Боварӣ ҳосил кунед, ки дар муодилаи кубӣ истилоҳи озод мавҷуд аст г{ Displaystyle d}. Агар дар муодилаи шакл ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ узви озод вуҷуд дорад ${ Displaystyle d}$ (ки ба сифр баробар нест), берун аз қавс гузоштани "x" кор намекунад. Дар ин ҳолат, усули дар ин бахш тавсифшударо истифода баред.
   • Масалан, бо назардошти муодилаи кубӣ ${ Displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Барои гирифтани сифр дар тарафи рости муодила, илова кунед ${ Displaystyle 6}$ ба ду тарафи муодила.
   • Муодила маълум мешавад ${ Displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Ҳамчун ${ Displaystyle d = 6}$, усули дар боби якум тавсифшударо истифода бурдан мумкин нест.
2. 2 Омилҳои коэффисиентро нависед а{ Displaystyle a} ва узви озод г{ Displaystyle d}. Яъне омилҳои рақамро дар ${ Displaystyle x ^ {3}}$ ва рақамҳо пеш аз аломати баробар. Дар хотир доред, ки омилҳои рақам рақамҳое мебошанд, ки ҳангоми зарб кардан ин рақамро ба вуҷуд меоранд.
   • Масалан, барои гирифтани рақам 6, шумо бояд зарб занед ${ Displaystyle 6 маротиба 1}$ ва ${ Displaystyle 2 маротиба 3}$... Пас рақамҳо 1, 2, 3, 6 омилҳои рақам мебошанд 6.
   • Дар муодилаи мо ${ Displaystyle a = 2}$ ва ${ Displaystyle d = 6}$... Зарбкунандаҳо 2 мебошанд 1 ва 2... Зарбкунандаҳо 6 рақамҳо мебошанд 1, 2, 3 ва 6.
3. 3 Ҳар як омилро тақсим кунед а{ Displaystyle a} барои ҳар як омил г{ Displaystyle d}. Дар натиҷа, шумо бисёр фраксияҳо ва якчанд ададҳоро мегиред; решаҳои муодилаи кубӣ яке аз ададҳо ё арзиши манфии яке аз ададҳо хоҳанд буд.
   • Дар мисоли мо, омилҳоро тақсим кунед ${ Displaystyle a}$ (1 ва 2) аз рӯи омилҳо ${ Displaystyle d}$ (1, 2, 3 ва 6). Шумо хоҳед гирифт: ${ Displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ Displaystyle 2}$ ва ${ displaystyle { frac {2} {3}}}$... Ҳоло ба ин рӯйхат қиматҳои манфии касрҳо ва рақамҳои гирифташударо илова кунед: ${ Displaystyle 1}$, ${ Displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ Displaystyle 2}$, ${ Displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ ва ${ displaystyle - { frac {2} {3}}}$... Тамоми решаҳои муодилаи кубӣ баъзе рақамҳо аз ин рӯйхат мебошанд.
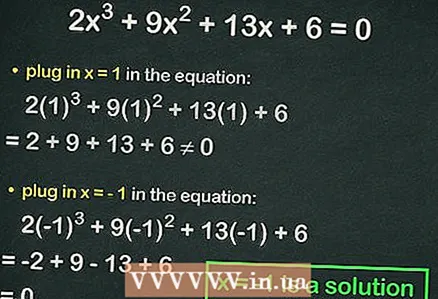4. 4 Ададҳоро ба муодилаи кубӣ пайваст кунед. Агар баробарӣ дуруст бошад, рақами ивазшуда решаи муодила аст. Масалан, дар муодила иваз кунед ${ Displaystyle 1}$:
   • ${ Displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ Displaystyle 2 + 9 + 13 + 6}$ ≠ 0, яъне баробарӣ риоя намешавад. Дар ин ҳолат рақами навбатиро пайваст кунед.
   • Иваз ${ Displaystyle -1}$: ${ Displaystyle (-2) +9 +(- 13) +6}$ = 0. Ҳамин тариқ, ${ Displaystyle -1}$ тамоми решаи муодила аст.
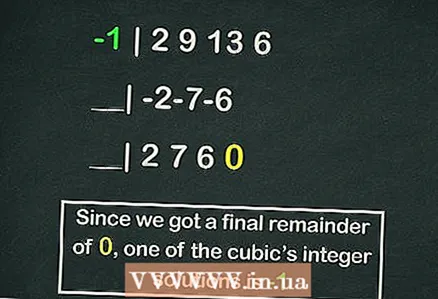5. 5 Усули тақсим кардани полиномаҳоро ба Нақшаи Hornerки решахои муодиларо тезтар ёбанд. Агар шумо нахоҳед, ки рақамҳоро ба муодила дастӣ иваз кунед, ин корро кунед. Дар нақшаи Ҳорнер, ададҳо ба қиматҳои коэффисиентҳои муодила тақсим карда мешаванд ${ Displaystyle a}$, ${ Displaystyle b}$, ${ Displaystyle c}$ ва ${ Displaystyle d}$... Агар рақамҳо баробар тақсим карда шаванд (яъне, боқимонда аст ${ Displaystyle 0}$), бутун решаи муодила аст.
   • Нақшаи Ҳорнер сазовори мақолаи алоҳида аст, аммо дар зер намунаи ҳисоб кардани яке аз решаҳои муодилаи кубии мо бо истифода аз ин схема оварда шудааст:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Пас боқимонда ҳамин тавр аст ${ Displaystyle 0}$, аммо ${ Displaystyle -1}$ яке аз решаҳои муодила аст.

Усули 3 аз 3: Чӣ тавр як муодиларо бо истифода аз дискриминант ҳал кардан мумкин аст

1. 1 Қиматҳои коэффисиентҳои муодиларо нависед а{ Displaystyle a}, б{ Displaystyle b}, в{ Displaystyle c} ва г{ Displaystyle d}. Мо тавсия медиҳем, ки шумо арзиши коэффисиентҳои зикршударо пешакӣ нависед, то дар оянда иштибоҳ накунед.
   • Масалан, бо назардошти муодила ${ Displaystyle x ^ {3} -3x ^ {2} + 3x -1}$... Навистан ${ Displaystyle a = 1}$, ${ Displaystyle b = -3}$, ${ Displaystyle c = 3}$ ва ${ Displaystyle d = -1}$... Ёдовар мешавем, ки агар пеш ${ Displaystyle x}$ рақам нест, коэффисиенти мувофиқ то ҳол вуҷуд дорад ва ба баробар аст ${ Displaystyle 1}$.
2. 2 Бо истифода аз формулаи махсус дискриминанти сифриро ҳисоб кунед. Барои ҳалли муодилаи кубӣ бо истифода аз дискриминант, шумо бояд як қатор ҳисобҳои душворро анҷом диҳед, аммо агар шумо ҳамаи қадамҳоро дуруст иҷро кунед, ин усул барои ҳалли муодилаҳои мураккаби мукааб ивазнашаванда мешавад. Аввал ҳисоб кардан ${ displaystyle Delta _ {0}}$ (дискриминант сифр) аввалин арзишест, ки ба мо лозим аст; Барои ин, дар формула арзишҳои мувофиқро иваз кунед ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • Дискриминант рақамест, ки решаҳои як полиномаро тавсиф мекунад (масалан, дискриминантсияи муодилаи квадратӣ бо формула ҳисоб карда мешавад ${ Displaystyle b ^ {2} -4ac}$).
   • Дар муодилаи мо:

     ${ Displaystyle b ^ {2} -3ac}$

     ${ Displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ Displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Бо истифода аз формула дискриминант якумро ҳисоб кунед Δ1=2б3−9абв+27а2г{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. Аввалин дискриминант ${ displaystyle Delta _ {1}}$ - ин арзиши дуввуми муҳим аст; Барои ҳисоб кардани он, арзишҳои мувофиқро ба формулаи муқарраршуда пайваст кунед.
   • Дар муодилаи мо:

     ${ Displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ Displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ Displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Дельта _ {1}}$

4. 4 Ҳисоб кунед:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Яъне, дискриминантсияи муодилаи кубиро тавассути арзишҳои бадастомада дарёфт кунед ${ displaystyle Delta _ {0}}$ ва ${ displaystyle Delta _ {1}}$... Агар дискриминантсияи муодилаи кубӣ мусбат бошад, муодила се реша дорад; агар дискриминант сифр бошад, муодила як ё ду реша дорад; агар табъиз манфӣ бошад, муодила як реша дорад.
   • Муодилаи кубӣ ҳамеша ҳадди аққал як реша дорад, зеро графи ин муодила ҳадди аққал дар як нуқта аз меҳвари X мегузарад.
   • Дар муодилаи мо ${ displaystyle Delta _ {0}}$ ва ${ displaystyle Delta _ {1}}$ баробаранд ${ Displaystyle 0}$, бинобар ин шумо метавонед ба осонӣ ҳисоб кунед ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ Displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ Displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... Ҳамин тариқ, муодилаи мо як ё ду реша дорад.

5. 5 Ҳисоб кунед:${ displaystyle C = ^ {3} { sqrt { чап ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } рост) div 2}}}$. ${ Displaystyle C}$ - ин охирин миқдори муҳимест, ки пайдо мешавад; он ба шумо дар ҳисоб кардани решаҳои муодила кӯмак мекунад. Арзишҳоро ба формулаи муқарраршуда иваз кунед ${ displaystyle Delta _ {1}}$ ва ${ displaystyle Delta _ {0}}$.
   • Дар муодилаи мо:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ Displaystyle 0 = C}$

6. 6 Се решаи муодиларо ёбед. Онро бо формула иҷро кунед ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, дар куҷо ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, аммо Н. баробар аст 1, 2 ё 3... Дар ин формула арзишҳои мувофиқро иваз кунед - дар натиҷа шумо се решаи муодиларо хоҳед гирифт.
   • Ҳисоб кардани арзиш бо формулаи дар Н. = 1, 2 ё 3ва сипас ҷавобро тафтиш кунед. Агар шумо ҳангоми санҷиши ҷавоби худ 0 гиред, ин арзиш решаи муодила аст.
   • Дар мисоли мо, иваз кунед 1 дар ${ Displaystyle x ^ {3} -3x ^ {2} + 3x -1}$ ва ба даст оред 0, яъне 1 яке аз решаҳои муодила аст.